华为宣布新芯片

测不准关系与傅里叶变换有关

测不准关系与傅里叶变换的关系解析

简介：

测不准关系是量子力学的核心原理之一，描述了在测量一个量的位置和动量时存在的固有不确定性。而傅里叶变换是一种数学方法，可将一个函数或信号从一个时域变换到另一个频域。本文将介绍测不准关系的概念和数学描述，并解释傅里叶变换与测不准关系之间的联系。

1. 测不准关系的概念和数学表达

测不准关系是基于海森堡的不确定性原理而提出的，它指出，在同一时刻，我们无法准确地知道一个粒子的位置和动量。根据测不准关系，位置和动量之间的测量不确定度满足以下关系式：

ΔxΔp ≥ ℏ/2

其中，Δx表示位置的不确定度，Δp表示动量的不确定度，ℏ为普朗克常数。

2. 傅里叶变换的概念和数学表达

傅里叶变换是一种将一个函数或信号从一个时域变换到另一个频域的方法，常用于信号处理、图像处理、通信等领域。傅里叶变换将一个函数表示为一组复数幅度和相位谱，可以将一个函数分解为一系列正弦和余弦波的和。傅里叶变换的公式为：

F(ω) = ∫f(t)e^(iωt)dt

其中，f(t)为输入函数，F(ω)为变换后的函数，ω为频率。

3. 测不准关系与傅里叶变换的联系

测不准关系和傅里叶变换之间的联系可以通过以下方式解释：

根据测不准关系，我们知道在一个粒子的位置和动量之间存在不确定性。在数学上，我们可以将粒子的位置看作一个时域函数，将粒子的动量看作一个频域函数。傅里叶变换正是将一个函数从时域变换到频域的方法，可以将一个位置函数转换为一个动量函数。

其次，傅里叶变换可以将一个函数表示为一组正弦和余弦波的和，而这些正弦和余弦波的频率与粒子的动量有直接的关系。因此，在进行测量时，我们无法同时准确地确定粒子的位置和动量，正是测不准关系的内容。

傅里叶变换还可以用于信号处理和频谱分析，而信号的频谱分析也涉及到位置和动量的测量。因此，傅里叶变换在测不准关系的研究和实际应用中起到了重要的作用。

结论：

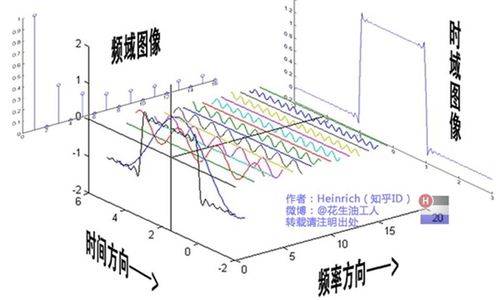
测不准关系和傅里叶变换之间存在着密切的联系。测不准关系描述了量子力学中位置和动量测量的不确定性，而傅里叶变换可以将一个函数从时域变换到频域，将位置函数转换为动量函数。因此，理解傅里叶变换对于理解测不准关系及其在量子力学中的应用具有重要意义。在实际应用中，傅里叶变换和测不准关系的结合可以用于信号处理、图像处理和频谱分析等领域，为解决相关问题提供了基础和参考。